An engineer uses a laser Doppler vibrometer to analyze the vibrations of a car in an anechoic room. The green laser beam is pointed at the car door to capture accurate vibration data. The car is placed in a special acoustic environment that allows measurements without external noise interference.

Signal processing: basics, techniques and applications

Signal processing involves the analysis and modification of signals to extract useful information in various applications.

Basics of signal processing

 

Signal processing is a wide-ranging field of engineering and computer science that deals with the analysis, modification and synthesis of signals in order to extract information from them. This information can be contained in the signal in the form of electrical, acoustic or imaging data, for example. The difference between digital signal processing and analog signal processing lies in the way in which the signals are processed. While analog signal processing deals with continuous signals, digital signal processing (DSP) works with discrete signals. The processing of digital signals is one of the prerequisites for today's digitalized world and has an impact on almost all areas of life.

Signal processing of sensor data

 

Data is often recorded as time signals from a wide variety of sensors. These sensors record physical phenomena such as temperature, pressure or light and convert them into electrical signals that can then be further processed. The ability to precisely record and analyze these signals is crucial for applications in medicine, communication technology, automation and many other areas. 

Digital and analog signal processing

Graphical representation of analog-to-digital conversion: An analog sine wave signal is converted into a digital signal. The top diagram shows the continuous analog signal, while the bottom diagram shows the quantized version of the signal after conversion into digital values.

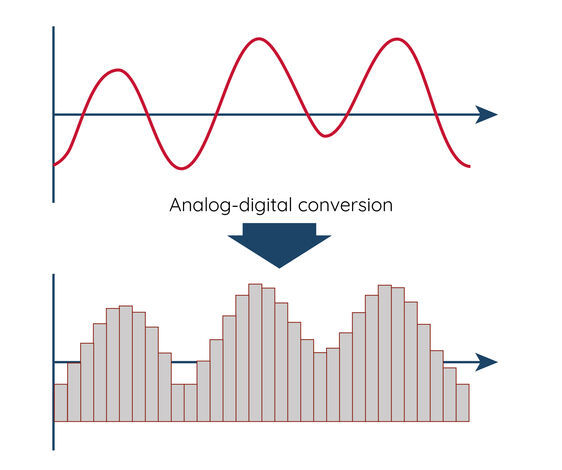
Before digital signal processing, continuous analog signals are converted into discrete digital signals by an analog-to-digital converter (ADC). These digital signals can then be processed with digital signal processors or computers. Digital signal processing offers several advantages: 

 

  • Reproducible and precise results: Environmental influences and component tolerances have little impact on data processing

     

  • Flexible possibilities: Fast development and inexpensive modification of signal processing

     

  • Simple implementation through the use of known algorithms

     

  • Secure storage and efficient transmission of digital data

     

  • Improved signal-to-noise ratio through adaptation to the data

     

Innovative signal processing in SMART Lab

Fundamentals and techniques of signal processing

 

Algorithms, for example for mixing, filtering, transforming or controlling a signal, form the basis of signal processing and combine various mathematical operators and concepts to generate a new signal from parts of one or more signals. Some important concepts are convolution, filtering and Fourier transformation.  

Convolution and digital signal processing filters
 

Convolution is a mathematical operator that combines two functions to produce a third function. In digital signal processing, convolution is often used to perform filter operations. Filters can take various forms such as low-pass, high-pass, band-pass or notch filters. They are used to remove unwanted frequency components from a signal or to emphasize certain frequency ranges. This improves the data during signal processing, for example by smoothing or noise suppression. 

Use of the Fourier transform
 

An essential part of signal processing is the Fourier transform, which transforms a signal from its time domain into the frequency domain. This technique is of central importance because many signals can be analyzed and manipulated more easily in the frequency domain. By using the Fast Fourier Transform (FFT), an efficient implementation of the Fourier transform, engineers can quickly identify and analyze the frequency components of a signal. 

Role of the difference equation in signal processing

 

An essential tool in signal processing is the difference equation. Difference equations are recursive equations that describe the current value of a discrete time series as a function of its previous values and the input values. They make it possible to systematically model and analyze the behaviour of a signal. In digital signal processing, difference equations are often used for the design and implementation of digital filters, as they provide a mathematically sound method for describing signal transformations. 

Mathematical representation

 

Difference equations are usually represented in the form y(n) = ∑k=0N ak x[n − k] + ∑m=1M bm y[n − m] where y(n) the current output value, x(n) the current input value, ak and bm are the filter coefficients. This equation shows how the current output value is determined by a weighted sum of the current and previous input values and the previous output values. By selecting suitable coefficients, different filter characteristics such as low-pass, high-pass, band-pass or band-stop filters can be realized.

Application in IIR and FIR filters

 

In practice, difference equations enable the implementation of Infinite Impulse Response (IIR) and Finite Impulse Response (FIR) filters. IIR filters, which are described by recursive difference equations, use both past input and output values and can achieve complex filter properties with less computational effort. FIR filters, on the other hand, only use past input values and are always stable, but are often more complex to calculate. 

Significance for digital signal processing
 

By using difference equations, digital filters can be precisely specified and efficiently implemented. This is particularly important in laser Doppler vibrometers, where large amounts of data are processed digitally with precision and in real time, and computing power is critical. The mathematical accuracy and flexibility offered by difference equations make them an indispensable tool in the development and application of modern signal processing algorithms. Their application makes it possible to analyze and manipulate complex signals, significantly improving the quality and efficiency of signal processing. 

Any questions? Contact us now!

Recap and prospects

 

In summary, signal processing is a diverse and deep field that encompasses numerous techniques and tools. From convolution in digital signal processing to the use of the Fourier transform, signal processing is the basis for many modern technologies and applications. The precise acquisition and processing of signals is essential in many technical and scientific fields and is constantly being further developed through continuous research and innovation.

Further topics on basics & measurement technology

Laser Source
Laser Vibrometry
Vibration measurement
Doppler Effect