Инженер использует лазерный доплеровский виброметр для анализа вибраций автомобиля в безэховой комнате. Зеленый лазерный луч направлен на дверь автомобиля, чтобы получить точные данные о вибрации. Автомобиль помещен в специальную акустическую среду, которая позволяет проводить измерения без внешних шумовых помех.

Обработка сигналов: основы, методы и приложения

Обработка сигналов включает в себя анализ и модификацию сигналов для извлечения полезной информации в различных приложениях.

Основы обработки сигналов

 

Обработка сигналов - это обширная область инженерных и компьютерных наук, которая занимается анализом, модификацией и синтезом сигналов с целью извлечения из них информации. Эта информация может содержаться в сигнале, например, в виде электрических, акустических или визуальных данных. Разница между цифровой и аналоговой обработкой сигналов заключается в способе обработки сигналов. В то время как аналоговая обработка сигналов имеет дело с непрерывными сигналами, цифровая обработка сигналов (DSP) работает с дискретными сигналами. Обработка цифровых сигналов является одной из предпосылок современного оцифрованного мира и оказывает влияние практически на все сферы жизни.

Обработка сигналов сенсорных данных

 

Данные часто записываются в виде временных сигналов от самых разных датчиков. Эти датчики регистрируют физические явления, такие как температура, давление или свет, и преобразуют их в электрические сигналы, которые затем могут быть обработаны. Способность точно регистрировать и анализировать эти сигналы имеет решающее значение для применения в медицине, коммуникационных технологиях, автоматизации и многих других областях.

Цифровая и аналоговая обработка сигналов

Графическое представление аналого-цифрового преобразования: Аналоговый синусоидальный сигнал преобразуется в цифровой. На верхней диаграмме показан непрерывный аналоговый сигнал, а на нижней - квантованная версия сигнала после преобразования в цифровые значения.

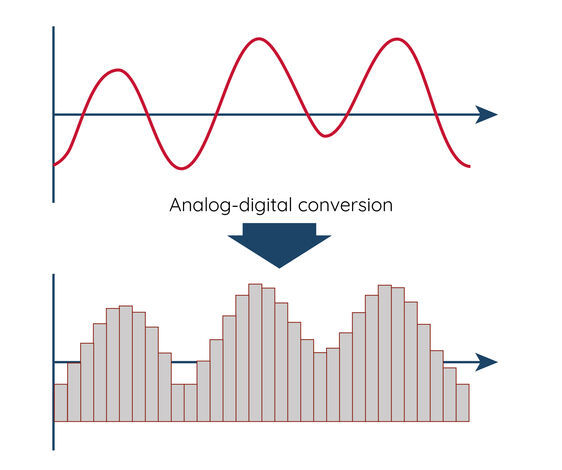
Перед цифровой обработкой сигналов непрерывные аналоговые сигналы преобразуются в дискретные цифровые сигналы с помощью аналого-цифрового преобразователя (АЦП). Затем эти цифровые сигналы могут быть обработаны с помощью цифровых сигнальных процессоров или компьютеров. Цифровая обработка сигналов имеет ряд преимуществ:

 

  • Воспроизводимые и точные результаты: Влияние окружающей среды и допуски компонентов практически не влияют на обработку данных

  • Гибкие возможности: Быстрая разработка и недорогая модификация системы обработки сигналов

  • Простая реализация за счет использования известных алгоритмов

  • Надежное хранение и эффективная передача цифровых данных

  • Улучшенное соотношение сигнал/шум благодаря адаптации к данным

Инновационная обработка сигналов в SMART Lab

Основы и методы обработки сигналов

 

Алгоритмы, например, для смешивания, фильтрации, преобразования или управления сигналом, составляют основу обработки сигналов и объединяют различные математические операторы и концепции для создания нового сигнала из частей одного или нескольких сигналов. Важными понятиями являются свертка, фильтрация и преобразование Фурье.

Конволюция и фильтры цифровой обработки сигналов

Свертка - это математический оператор, который объединяет две функции для получения третьей функции. В цифровой обработке сигналов свертка часто используется для выполнения операций с фильтрами. Фильтры могут иметь различные формы, такие как фильтры низких и высоких частот, полосовые фильтры или фильтры с засечками. Они используются для удаления нежелательных частотных компонентов из сигнала или для выделения определенных частотных диапазонов. Это позволяет улучшить данные при обработке сигнала, например, за счет сглаживания или подавления шума.

Использование преобразования Фурье

Важнейшей частью обработки сигналов является преобразование Фурье, которое переводит сигнал из временной области в частотную. Эта техника имеет огромное значение, поскольку многие сигналы легче анализировать и манипулировать ими в частотной области. Используя быстрое преобразование Фурье (БПФ), эффективную реализацию преобразования Фурье, инженеры могут быстро определять и анализировать частотные компоненты сигнала.

Роль разностного уравнения в обработке сигналов

 

Важнейшим инструментом в обработке сигналов является разностное уравнение. Разностные уравнения - это рекурсивные уравнения, которые описывают текущее значение дискретного временного ряда как функцию его предыдущих значений и входных значений. Они позволяют систематически моделировать и анализировать поведение сигнала. В цифровой обработке сигналов разностные уравнения часто используются для проектирования и реализации цифровых фильтров, поскольку они обеспечивают математически обоснованный метод описания преобразований сигнала.

Математическое представление

 

Разностные уравнения обычно представляются в виде y(n) = ∑k=0Nak x[n - k] + ∑m=1Mbm y[n - m], где y(n) - текущее выходное значение, x(n) - текущее входное значение, ak и bm - коэффициенты фильтра. Это уравнение показывает, как текущее выходное значение определяется взвешенной суммой текущего и предыдущего входных значений и предыдущих выходных значений. Выбирая подходящие коэффициенты, можно реализовать различные характеристики фильтров, такие как низкочастотные, высокочастотные, полосовые или полосно-стопные.

Применение в фильтрах IIR и FIR

 

На практике разностные уравнения позволяют реализовать фильтры с бесконечным импульсным откликом (IIR) и с конечным импульсным откликом (FIR). IIR-фильтры, которые описываются рекурсивными разностными уравнениями, используют как прошлые входные, так и выходные значения и позволяют добиться сложных свойств фильтра при меньших вычислительных затратах. FIR-фильтры, с другой стороны, используют только прошлые входные значения и всегда стабильны, но часто более сложны для вычисления.

Значение для цифровой обработки сигналов

Использование разностных уравнений позволяет точно определить и эффективно реализовать цифровые фильтры. Это особенно важно для лазерных доплеровских виброметров, где большие объемы данных обрабатываются в цифровом виде с высокой точностью и в режиме реального времени, а вычислительная мощность имеет решающее значение. Математическая точность и гибкость разностных уравнений делают их незаменимым инструментом при разработке и применении современных алгоритмов обработки сигналов. Их применение позволяет анализировать и манипулировать сложными сигналами, значительно повышая качество и эффективность обработки сигналов.

Есть вопросы? Свяжитесь с нами прямо сейчас!

Итоги и перспективы

 

В целом, обработка сигналов - это разнообразная и глубокая область, которая включает в себя множество методов и инструментов. От свертки в цифровой обработке сигналов до использования преобразования Фурье - обработка сигналов является основой для многих современных технологий и приложений. Точный сбор и обработка сигналов необходимы во многих технических и научных областях, и они постоянно совершенствуются благодаря непрерывным исследованиям и инновациям.

Другие темы по основам и измерительной технике

Источник лазерного излучения
Лазерная виброметрия
Измерение вибрации
Эффект Доплера