Inżynier używa laserowego wibrometru dopplerowskiego do analizy drgań samochodu w pomieszczeniu bezechowym. Zielona wiązka lasera jest skierowana na drzwi samochodu w celu uzyskania dokładnych danych dotyczących drgań. Samochód jest umieszczony w specjalnym środowisku akustycznym, które umożliwia pomiary bez zakłóceń zewnętrznych.

Przetwarzanie sygnałów: podstawy, techniki i zastosowania

Przetwarzanie sygnałów obejmuje analizę i modyfikację sygnałów w celu wydobycia użytecznych informacji w różnych zastosowaniach.

Podstawy przetwarzania sygnałów

 

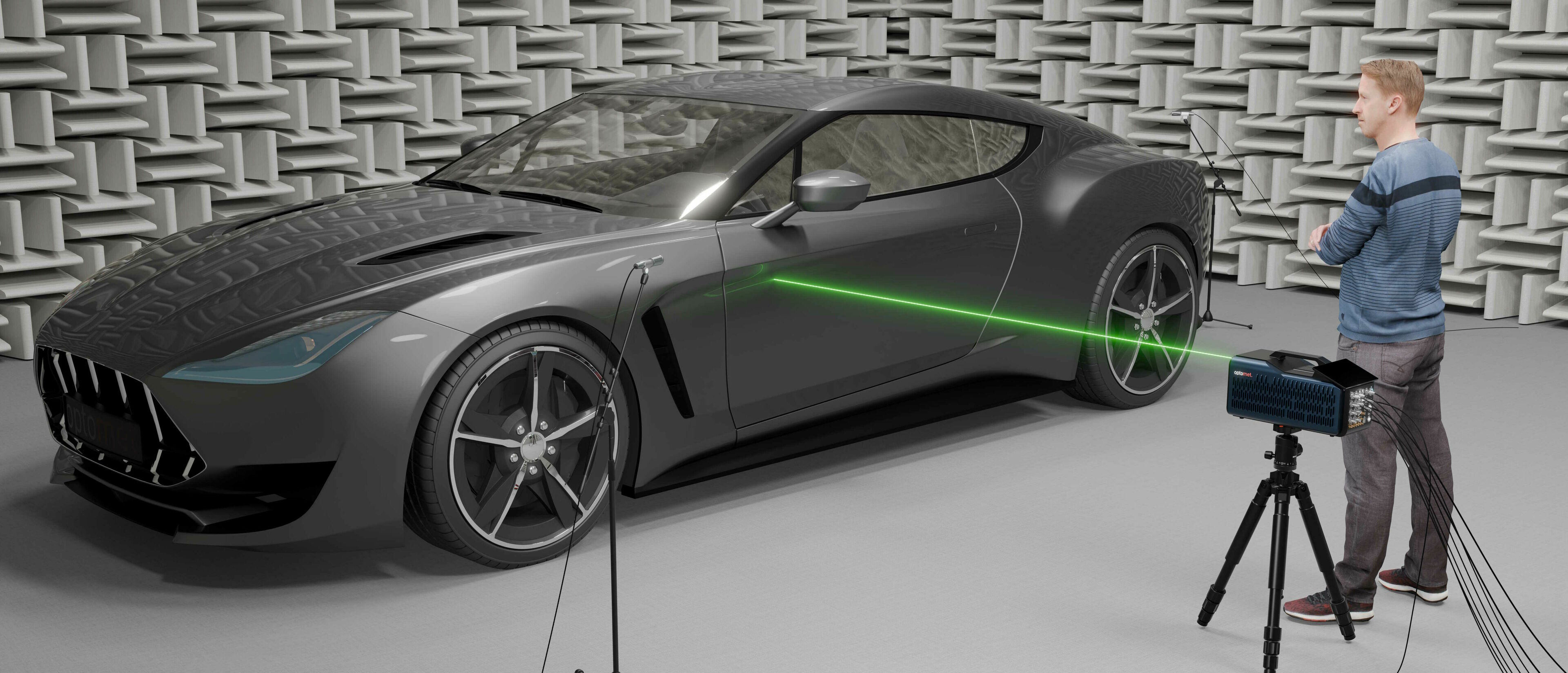
Przetwarzanie sygnałów to szeroko zakrojona dziedzina inżynierii i informatyki, która zajmuje się analizą, modyfikacją i syntezą sygnałów w celu wydobycia z nich informacji. Informacje te mogą być zawarte w sygnale, na przykład w postaci danych elektrycznych, akustycznych lub obrazowych. Różnica między cyfrowym przetwarzaniem sygnałów a przetwarzaniem sygnałów analogowych polega na sposobie przetwarzania sygnałów. Podczas gdy analogowe przetwarzanie sygnałów zajmuje się sygnałami ciągłymi, cyfrowe przetwarzanie sygnałów (DSP) działa z sygnałami dyskretnymi. Przetwarzanie sygnałów cyfrowych jest jednym z warunków wstępnych dzisiejszego zdigitalizowanego świata i ma wpływ na prawie wszystkie dziedziny życia.

Przetwarzanie sygnałów z czujników

 

Dane są często rejestrowane jako sygnały czasowe z wielu różnych czujników. Czujniki te rejestrują zjawiska fizyczne, takie jak temperatura, ciśnienie lub światło i przekształcają je w sygnały elektryczne, które mogą być następnie przetwarzane. Zdolność do precyzyjnego rejestrowania i analizowania tych sygnałów ma kluczowe znaczenie dla zastosowań w medycynie, technologii komunikacyjnej, automatyce i wielu innych dziedzinach.

Cyfrowe i analogowe przetwarzanie sygnałów

Graficzne przedstawienie konwersji analogowo-cyfrowej: Analogowy sygnał sinusoidalny jest konwertowany na sygnał cyfrowy. Górny wykres przedstawia ciągły sygnał analogowy, natomiast dolny wykres przedstawia skwantowaną wersję sygnału po konwersji na wartości cyfrowe.

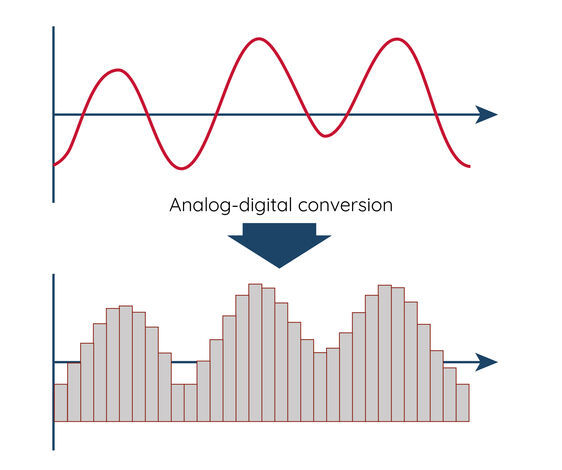
Przed cyfrowym przetwarzaniem sygnału, ciągłe sygnały analogowe są konwertowane na dyskretne sygnały cyfrowe za pomocą przetwornika analogowo-cyfrowego (ADC). Te sygnały cyfrowe mogą być następnie przetwarzane przez procesory sygnałów cyfrowych lub komputery. Cyfrowe przetwarzanie sygnałów ma kilka zalet:

 

  • Powtarzalne i precyzyjne wyniki: Wpływ środowiska i tolerancje komponentów mają niewielki wpływ na przetwarzanie danych

  • Elastyczne możliwości: Szybki rozwój i niedroga modyfikacja przetwarzania sygnału

  • Prosta implementacja dzięki wykorzystaniu znanych algorytmów

  • Bezpieczne przechowywanie i wydajna transmisja danych cyfrowych

  • Lepszy stosunek sygnału do szumu dzięki adaptacji do danych

Innowacyjne przetwarzanie sygnału w SMART Lab

Podstawy i techniki przetwarzania sygnałów

 

Algorytmy, na przykład do mieszania, filtrowania, przekształcania lub kontrolowania sygnału, stanowią podstawę przetwarzania sygnału i łączą różne operatory matematyczne i koncepcje w celu wygenerowania nowego sygnału z części jednego lub więcej sygnałów. Niektóre ważne pojęcia to splot, filtrowanie i transformacja Fouriera.

Konwolucja i filtry cyfrowego przetwarzania sygnałów

Konwolucja to operator matematyczny, który łączy dwie funkcje w celu uzyskania trzeciej funkcji. W cyfrowym przetwarzaniu sygnałów splot jest często używany do wykonywania operacji filtrowania. Filtry mogą przybierać różne formy, takie jak filtry dolnoprzepustowe, górnoprzepustowe, pasmowo-przepustowe lub wycinające. Służą one do usuwania niepożądanych składowych częstotliwości z sygnału lub do podkreślania określonych zakresów częstotliwości. Poprawia to jakość danych podczas przetwarzania sygnału, na przykład poprzez wygładzanie lub tłumienie szumów.

Wykorzystanie transformaty Fouriera

Istotną częścią przetwarzania sygnałów jest transformata Fouriera, która przekształca sygnał z dziedziny czasu w dziedzinę częstotliwości. Technika ta ma kluczowe znaczenie, ponieważ wiele sygnałów można łatwiej analizować i manipulować nimi w dziedzinie częstotliwości. Korzystając z szybkiej transformaty Fouriera (FFT), wydajnej implementacji transformaty Fouriera, inżynierowie mogą szybko identyfikować i analizować składowe częstotliwościowe sygnału.

Rola równania różniczkowego w przetwarzaniu sygnałów

 

Niezbędnym narzędziem w przetwarzaniu sygnałów jest równanie różniczkowe. Równania różnicowe są równaniami rekurencyjnymi, które opisują bieżącą wartość dyskretnego szeregu czasowego jako funkcję jego poprzednich wartości i wartości wejściowych. Umożliwiają one systematyczne modelowanie i analizowanie zachowania sygnału. W cyfrowym przetwarzaniu sygnałów równania różniczkowe są często wykorzystywane do projektowania i implementacji filtrów cyfrowych, ponieważ zapewniają matematycznie uzasadnioną metodę opisu transformacji sygnału.

Reprezentacja matematyczna

 

Równania różniczkowe są zwykle przedstawiane w postaci y(n) = ∑k=0Nak x[n - k] + ∑m=1Mbm y[n - m] gdzie y(n) bieżąca wartość wyjściowa, x(n) bieżąca wartość wejściowa,ak i bm są współczynnikami filtra. Równanie to pokazuje, w jaki sposób bieżąca wartość wyjściowa jest określana przez ważoną sumę bieżącej i poprzedniej wartości wejściowej oraz poprzedniej wartości wyjściowej. Wybierając odpowiednie współczynniki, można uzyskać różne charakterystyki filtrów, takie jak filtry dolnoprzepustowe, górnoprzepustowe, pasmowo-przepustowe lub pasmowo-zaporowe.

Zastosowanie w filtrach IIR i FIR

 

W praktyce równania różniczkowe umożliwiają implementację filtrów o nieskończonej odpowiedzi impulsowej (IIR) i skończonej odpowiedzi impulsowej (FIR). Filtry IIR, które są opisane przez rekurencyjne równania różniczkowe, wykorzystują zarówno przeszłe wartości wejściowe, jak i wyjściowe i mogą osiągnąć złożone właściwości filtra przy mniejszym wysiłku obliczeniowym. Z drugiej strony filtry FIR wykorzystują tylko przeszłe wartości wejściowe i są zawsze stabilne, ale często są bardziej złożone w obliczeniach.

Znaczenie dla cyfrowego przetwarzania sygnałów

Dzięki zastosowaniu równań różniczkowych filtry cyfrowe mogą być precyzyjnie określone i wydajnie zaimplementowane. Jest to szczególnie ważne w laserowych wibrometrach dopplerowskich, gdzie duże ilości danych są przetwarzane cyfrowo z precyzją i w czasie rzeczywistym, a moc obliczeniowa ma krytyczne znaczenie. Matematyczna dokładność i elastyczność równań różniczkowych sprawiają, że są one niezbędnym narzędziem w opracowywaniu i stosowaniu nowoczesnych algorytmów przetwarzania sygnałów. Ich zastosowanie umożliwia analizowanie i manipulowanie złożonymi sygnałami, znacznie poprawiając jakość i wydajność przetwarzania sygnałów.

Masz pytania? Skontaktuj się z nami teraz!

Podsumowanie i perspektywy

 

Podsumowując, przetwarzanie sygnałów jest zróżnicowaną i głęboką dziedziną, która obejmuje wiele technik i narzędzi. Od splotu w cyfrowym przetwarzaniu sygnałów po wykorzystanie transformaty Fouriera, przetwarzanie sygnałów jest podstawą wielu nowoczesnych technologii i aplikacji. Precyzyjne pozyskiwanie i przetwarzanie sygnałów jest niezbędne w wielu dziedzinach technicznych i naukowych i jest stale rozwijane poprzez ciągłe badania i innowacje.

Dalsze tematy dotyczące podstaw i technologii pomiarowych

Źródło lasera
Wibrometria laserowa
Pomiar wibracji
Efekt Dopplera