信号処理

フォトディテクターから信頼性の高い測定値へ：復調、フィルタリング、サンプリングレート、FFT、ノイズフロアが振動データの品質を左右します。

1 分で読めます振動測定と信号解析

信号処理では、信号を解析・加工することで、さまざまな用途に有用な情報を抽出します。

信号処理の基礎

信号処理は、工学および情報科学にまたがる幅広い分野であり、信号を解析、加工、合成して情報を抽出する技術です。信号には、電気、音響、画像などのデータとして情報が含まれています。デジタル信号処理とアナログ信号処理の違いは、信号の処理方法にあります。アナログ信号処理が連続信号を扱うのに対し、デジタル信号処理（DSP）は離散信号を扱います。デジタル信号の処理技術は、現代のデジタル社会を支える基盤の1つであり、生活のほぼあらゆる領域に影響を及ぼしています。

センサーデータの信号処理

データは、多種多様なセンサーによって時系列信号として記録されることが一般的です。これらのセンサーは、温度、圧力、光などの物理現象を検出し、後続処理が可能な電気信号へ変換します。こうした信号を正確に取得・解析する技術は、医療、通信技術、オートメーションをはじめとする幅広い分野のアプリケーションに不可欠です。

デジタル信号処理とアナログ信号処理

アナログ信号からデジタル信号への変換図。 — アナログ信号からデジタル信号への変換

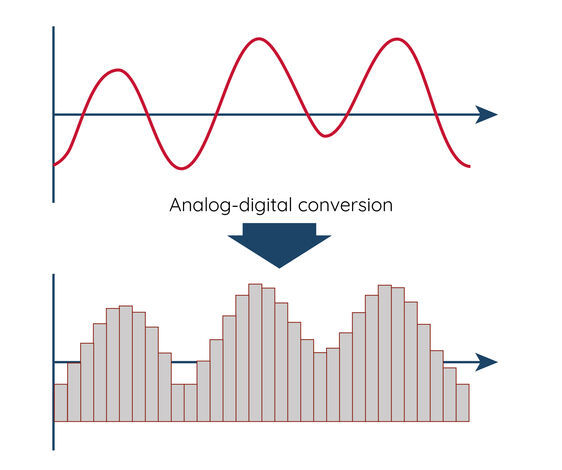
デジタル信号処理を行う前に、連続的なアナログ信号をアナログデジタル変換器（ADC）によって離散的なデジタル信号に変換します。変換されたデジタル信号は、デジタルシグナルプロセッサやコンピューターで処理できます。デジタル信号処理には、次のような利点があります。

再現性に優れた高精度な結果：環境要因や部品公差がデータ処理に及ぼす影響を抑制
高い柔軟性：信号処理を迅速に開発でき、低コストで変更可能
既知のアルゴリズムを使用することで容易に実装可能
デジタルデータの安全な保存と効率的な伝送
データに応じた最適化による信号対雑音比の向上

信号処理の基礎と手法

信号のミキシング、フィルタリング、変換、制御などを行うアルゴリズムは、信号処理の基礎を成すものです。さまざまな数学的演算子や概念を組み合わせ、1つまたは複数の信号の一部から新たな信号を生成します。重要な概念として、畳み込み、フィルタリング、フーリエ変換などがあります。

畳み込みとデジタル信号処理フィルター

畳み込みは、2つの関数を組み合わせて第3の関数を生成する数学的演算です。デジタル信号処理では、フィルター処理を行うために畳み込みが多く用いられます。フィルターには、ローパス、ハイパス、バンドパス、ノッチなど、さまざまな種類があります。これらは、信号から不要な周波数成分を除去したり、特定の周波数帯域を強調したりするために使用されます。これにより、平滑化やノイズ低減などを通じて、信号処理におけるデータ品質を向上できます。

フーリエ変換の活用

信号処理の主要な要素の1つが、信号を時間領域から周波数領域へ変換するフーリエ変換です。多くの信号は周波数領域の方が解析や処理を容易に行えるため、この手法は極めて重要です。フーリエ変換を効率的に実行する高速フーリエ変換（FFT）を用いることで、技術者は信号の周波数成分を迅速に特定し、解析できます。

信号処理における差分方程式の役割

差分方程式は、信号処理に欠かせない手法の1つです。差分方程式とは、離散時系列の現在値を、過去の値と入力値に基づいて表す再帰方程式です。これにより、信号の挙動を体系的にモデル化し、解析できます。差分方程式は信号変換を数学的根拠に基づいて記述できるため、デジタル信号処理ではデジタルフィルターの設計や実装に広く用いられています。

数学的表現

差分方程式は通常、y(n) = ∑ₖ₌₀ᴺ aₖ x[n−k] + ∑ₘ₌₁ᴹ bₘ y[n−m] の形式で表されます。ここで、y(n) は現在の出力値、x(n) は現在の入力値、ak および bm はフィルタ係数です。この方程式は、現在および過去の入力値と過去の出力値の重み付き和によって、現在の出力値がどのように決定されるかを示しています。適切な係数を選択することで、ローパス、ハイパス、バンドパス、バンドストップなど、さまざまなフィルタ特性を実現できます。

IIRフィルタおよびFIRフィルタへの適用

実際には、差分方程式を用いることで、無限インパルス応答（Infinite Impulse Response, IIR）フィルタと有限インパルス応答（Finite Impulse Response, FIR）フィルタを実装できます。再帰型差分方程式で表されるIIRフィルタは、過去の入力値と出力値の両方を使用し、少ない計算量で複雑なフィルタ特性を実現できます。一方、FIRフィルタは過去の入力値のみを使用するため常に安定していますが、多くの場合、計算量が増大します。

デジタル信号処理における重要性

差分方程式を用いることで、デジタルフィルタを正確に定義し、効率的に実装できます。これは特に、レーザドップラ振動計では特に重要です。大量のデータを高精度かつリアルタイムにデジタル処理する必要があり、演算性能が決定的な役割を果たすためです。差分方程式は数学的な精度と柔軟性を備えており、最新の信号処理アルゴリズムの開発と応用に欠かせないツールです。差分方程式を適用することで複雑な信号の解析と操作が可能になり、信号処理の品質と効率を大幅に向上できます。

まとめと今後の展望

まとめると、信号処理は多様かつ広範な分野であり、数多くの手法やツールが含まれます。デジタル信号処理における畳み込みからフーリエ変換の利用に至るまで、信号処理は多くの最新技術とアプリケーションを支える基盤です。信号の正確な取得と処理は、さまざまな技術・科学分野に不可欠であり、継続的な研究とイノベーションによって絶えず進化しています。