Un ingénieur utilise un vibromètre laser Doppler pour analyser les vibrations d'une voiture dans une salle anéchoïque. Le faisceau laser vert est dirigé vers la portière de la voiture afin d'obtenir des données précises sur les vibrations. La voiture est placée dans un environnement acoustique spécial qui permet d'effectuer des mesures sans interférences sonores externes.

Traitement du signal : bases, techniques et applications

Le traitement du signal implique l'analyse et la modification des signaux pour en extraire des informations utiles dans diverses applications.

Principes de base du traitement des signaux

 

Le traitement du signal est un vaste domaine de l'ingénierie et de l'informatique qui traite de l'analyse, de la modification et de la synthèse des signaux afin d'en extraire des informations. Ces informations peuvent être contenues dans le signal sous la forme de données électriques, acoustiques ou d'imagerie, par exemple. La différence entre le traitement numérique des signaux et le traitement analogique des signaux réside dans la manière dont les signaux sont traités. Alors que le traitement des signaux analogiques traite des signaux continus, le traitement des signaux numériques (DSP) traite des signaux discrets. Le traitement des signaux numériques est l'une des conditions préalables au monde numérisé d'aujourd'hui et a un impact sur presque tous les domaines de la vie.

Traitement des signaux des données des capteurs

 

Les données sont souvent enregistrées sous forme de signaux temporels provenant d'une grande variété de capteurs. Ces capteurs enregistrent des phénomènes physiques tels que la température, la pression ou la lumière et les convertissent en signaux électriques qui peuvent ensuite être traités. La capacité d'enregistrer et d'analyser ces signaux avec précision est cruciale pour les applications dans les domaines de la médecine, des technologies de la communication, de l'automatisation et dans bien d'autres domaines.

Traitement des signaux numériques et analogiques

Représentation graphique de la conversion analogique-numérique : Un signal sinusoïdal analogique est converti en un signal numérique. Le diagramme du haut montre le signal analogique continu, tandis que le diagramme du bas montre la version quantifiée du signal après conversion en valeurs numériques.

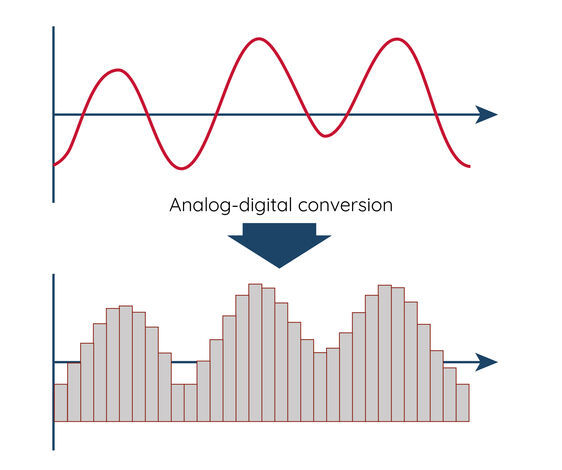
Avant le traitement des signaux numériques, les signaux analogiques continus sont convertis en signaux numériques discrets par un convertisseur analogique-numérique (ADC). Ces signaux numériques peuvent ensuite être traités par des processeurs de signaux numériques ou des ordinateurs. Le traitement numérique des signaux offre plusieurs avantages :

 

  • Résultats reproductibles et précis : Les influences environnementales et les tolérances des composants ont peu d'impact sur le traitement des données.

  • Possibilités flexibles : Développement rapide et modification peu coûteuse du traitement des signaux

  • Mise en œuvre simple grâce à l'utilisation d'algorithmes connus

  • Stockage sécurisé et transmission efficace des données numériques

  • Amélioration du rapport signal/bruit grâce à l'adaptation aux données

Traitement innovant des signaux dans le SMART Lab

Principes fondamentaux et techniques du traitement des signaux

 

Les algorithmes, par exemple pour mélanger, filtrer, transformer ou contrôler un signal, constituent la base du traitement des signaux et combinent divers opérateurs et concepts mathématiques pour générer un nouveau signal à partir de parties d'un ou de plusieurs signaux. Certains concepts importants sont la convolution, le filtrage et la transformation de Fourier.

Convolution et filtres de traitement des signaux numériques

La convolution est un opérateur mathématique qui combine deux fonctions pour en produire une troisième. Dans le traitement des signaux numériques, la convolution est souvent utilisée pour effectuer des opérations de filtrage. Les filtres peuvent prendre différentes formes, telles que les filtres passe-bas, passe-haut, passe-bande ou coupe-bande. Ils sont utilisés pour éliminer les composantes de fréquence indésirables d'un signal ou pour accentuer certaines plages de fréquence. Cela permet d'améliorer les données lors du traitement des signaux, par exemple en les lissant ou en supprimant le bruit.

Utilisation de la transformée de Fourier

La transformée de Fourier, qui transforme un signal du domaine temporel au domaine fréquentiel, est un élément essentiel du traitement des signaux. Cette technique est d'une importance capitale car de nombreux signaux peuvent être analysés et manipulés plus facilement dans le domaine des fréquences. En utilisant la transformée de Fourier rapide (FFT), une implémentation efficace de la transformée de Fourier, les ingénieurs peuvent rapidement identifier et analyser les composantes de fréquence d'un signal.

Rôle de l'équation de différence dans le traitement des signaux

 

L'équation de différence est un outil essentiel dans le traitement des signaux. Les équations de différence sont des équations récursives qui décrivent la valeur actuelle d'une série temporelle discrète en fonction de ses valeurs précédentes et des valeurs d'entrée. Elles permettent de modéliser et d'analyser systématiquement le comportement d'un signal. Dans le traitement des signaux numériques, les équations de différence sont souvent utilisées pour la conception et la mise en œuvre de filtres numériques, car elles fournissent une méthode mathématiquement solide pour décrire les transformations du signal.

Représentation mathématique

 

Les équations différentielles sont généralement représentées sous la forme y(n) = ∑k=0Nak x[n - k] + ∑m=1Mbm y[n - m] où y(n) est la valeur de sortie actuelle, x(n) la valeur d'entrée actuelle, ak et bm sont les coefficients du filtre. Cette équation montre comment la valeur de sortie actuelle est déterminée par une somme pondérée des valeurs d'entrée actuelles et précédentes et des valeurs de sortie précédentes. En sélectionnant les coefficients appropriés, il est possible de réaliser différentes caractéristiques de filtre telles que des filtres passe-bas, passe-haut, passe-bande ou coupe-bande.

Application aux filtres IIR et FIR

 

Dans la pratique, les équations de différence permettent la mise en œuvre de filtres à réponse impulsionnelle infinie (IIR) et à réponse impulsionnelle finie (FIR). Les filtres IIR, qui sont décrits par des équations de différence récursives, utilisent à la fois les valeurs d'entrée et de sortie passées et permettent d'obtenir des propriétés de filtrage complexes avec un effort de calcul moindre. Les filtres FIR, quant à eux, n'utilisent que les valeurs d'entrée passées et sont toujours stables, mais ils sont souvent plus complexes à calculer.

Importance pour le traitement des signaux numériques

L'utilisation d'équations de différence permet de spécifier avec précision les filtres numériques et de les mettre en œuvre efficacement. Ceci est particulièrement important dans les vibromètres laser Doppler, où de grandes quantités de données sont traitées numériquement avec précision et en temps réel, et où la puissance de calcul est critique. La précision mathématique et la flexibilité offertes par les équations aux différences en font un outil indispensable au développement et à l'application d'algorithmes modernes de traitement des signaux. Leur application permet d'analyser et de manipuler des signaux complexes, ce qui améliore considérablement la qualité et l'efficacité du traitement des signaux.

Vous avez des questions ? Contactez nous dès maintenant !

Bilan et perspectives

 

En résumé, le traitement du signal est un domaine varié et profond qui englobe de nombreuses techniques et de nombreux outils. De la convolution dans le traitement des signaux numériques à l'utilisation de la transformée de Fourier, le traitement des signaux est à la base de nombreuses technologies et applications modernes. L'acquisition et le traitement précis des signaux sont essentiels dans de nombreux domaines techniques et scientifiques et sont constamment perfectionnés grâce à la recherche et à l'innovation.

Autres thèmes sur les bases et la technologie de mesure

Source laser
Vibrométrie laser
Mesure des vibrations
Effet Doppler