Un ingeniero utiliza un vibrómetro láser Doppler para analizar las vibraciones de un coche en una sala anecoica. El rayo láser verde apunta a la puerta del coche para captar datos precisos sobre las vibraciones. El coche se coloca en un entorno acústico especial que permite realizar mediciones sin interferencias de ruido externo.

Procesado de señales: fundamentos, técnicas y aplicaciones

El procesamiento de señales consiste en analizarlas y modificarlas para extraer información útil en diversas aplicaciones.

Fundamentos del tratamiento de señales

 

El tratamiento de señales es un amplio campo de la ingeniería y la informática que se ocupa del análisis, la modificación y la síntesis de señales para extraer información de ellas. Esta información puede estar contenida en la señal en forma de datos eléctricos, acústicos o de imagen, por ejemplo. La diferencia entre el tratamiento digital de señales y el analógico radica en la forma en que se procesan las señales. Mientras que el tratamiento analógico de señales trabaja con señales continuas, el tratamiento digital de señales (DSP) lo hace con señales discretas. El procesamiento de señales digitales es uno de los requisitos previos del mundo digitalizado actual y tiene repercusiones en casi todos los ámbitos de la vida.

Tratamiento de señales de datos de sensores

 

Los datos suelen registrarse en forma de señales temporales procedentes de una gran variedad de sensores. Estos sensores registran fenómenos físicos como la temperatura, la presión o la luz y los convierten en señales eléctricas que pueden procesarse posteriormente. La capacidad de registrar y analizar con precisión estas señales es crucial para aplicaciones en medicina, tecnología de la comunicación, automatización y muchas otras áreas.

Tratamiento de señales digitales y analógicas

Representación gráfica de la conversión analógico-digital: Una señal analógica sinusoidal se convierte en una señal digital. El diagrama superior muestra la señal analógica continua, mientras que el diagrama inferior muestra la versión cuantizada de la señal tras la conversión en valores digitales.

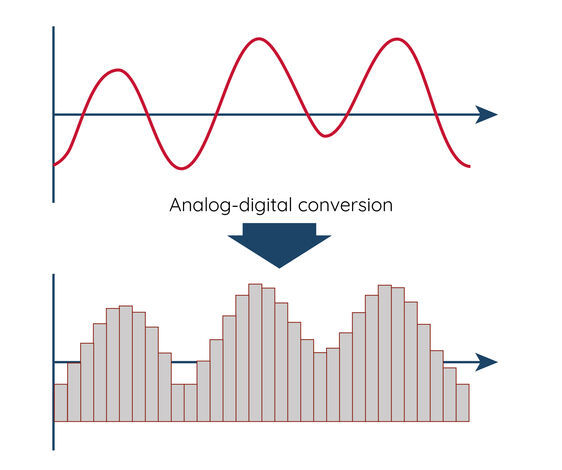
Antes de procesar una señal digital, un convertidor analógico-digital (ADC) convierte las señales analógicas continuas en señales digitales discretas. A continuación, estas señales digitales pueden procesarse con procesadores de señales digitales u ordenadores. El procesamiento digital de señales ofrece varias ventajas:

 

  • Resultados reproducibles y precisos: Las influencias ambientales y las tolerancias de los componentes apenas afectan al procesamiento de los datos.

  • Posibilidades flexibles: Desarrollo rápido y modificación económica del procesamiento de señales.

  • Implementación sencilla mediante el uso de algoritmos conocidos

  • Almacenamiento seguro y transmisión eficaz de datos digitales

  • Mejora de la relación señal/ruido mediante la adaptación a los datos

Procesamiento innovador de señales en SMART Lab

Fundamentos y técnicas del tratamiento de señales

 

Los algoritmos, por ejemplo para mezclar, filtrar, transformar o controlar una señal, constituyen la base del tratamiento de señales y combinan diversos operadores y conceptos matemáticos para generar una nueva señal a partir de partes de una o varias señales. Algunos conceptos importantes son la convolución, el filtrado y la transformación de Fourier.

Convolución y filtros de procesamiento digital de señales

La convolución es un operador matemático que combina dos funciones para producir una tercera función. En el procesamiento digital de señales, la convolución se utiliza a menudo para realizar operaciones de filtrado. Los filtros pueden ser de paso bajo, paso alto, paso banda o notch. Se utilizan para eliminar componentes de frecuencia no deseados de una señal o para enfatizar determinados rangos de frecuencia. De este modo se mejoran los datos durante el procesamiento de la señal, por ejemplo, mediante el suavizado o la supresión del ruido.

Utilización de la transformada de Fourier

Una parte esencial del tratamiento de señales es la transformada de Fourier, que transforma una señal de su dominio temporal al dominio de la frecuencia. Esta técnica es de vital importancia porque muchas señales pueden analizarse y manipularse más fácilmente en el dominio de la frecuencia. Mediante el uso de la transformada rápida de Fourier (FFT), una implementación eficiente de la transformada de Fourier, los ingenieros pueden identificar y analizar rápidamente los componentes de frecuencia de una señal.

Función de la ecuación en diferencias en el tratamiento de señales

 

Una herramienta esencial en el tratamiento de señales es la ecuación en diferencias. Las ecuaciones en diferencias son ecuaciones recursivas que describen el valor actual de una serie temporal discreta en función de sus valores anteriores y de los valores de entrada. Permiten modelar y analizar sistemáticamente el comportamiento de una señal. En el procesamiento digital de señales, las ecuaciones en diferencias se utilizan a menudo para el diseño y la implementación de filtros digitales, ya que proporcionan un método matemáticamente sólido para describir las transformaciones de la señal.

Representación matemática

 

Las ecuaciones diferenciales suelen representarse de la forma y(n) = ∑k=0Nak x[n - k] + ∑m=1Mbm y[n - m] donde y(n) es el valor de salida actual, x(n) el valor de entrada actual, ak y bm son los coeficientes del filtro. Esta ecuación muestra cómo se determina el valor de salida actual mediante una suma ponderada de los valores de entrada actual y anterior y los valores de salida anteriores. Seleccionando los coeficientes adecuados, se pueden conseguir diferentes características de filtro, como filtros pasa-bajos, pasa-altos, pasa-banda o pasa-banda.

Aplicación en filtros IIR y FIR

 

En la práctica, las ecuaciones en diferencias permiten implementar filtros de respuesta infinita al impulso (IIR) y de respuesta finita al impulso (FIR). Los filtros IIR, que se describen mediante ecuaciones en diferencias recursivas, utilizan valores de entrada y salida pasados y pueden conseguir propiedades de filtro complejas con menos esfuerzo computacional. Los filtros FIR, en cambio, sólo utilizan valores de entrada pasados y son siempre estables, pero suelen ser más complejos de calcular.

Importancia para el procesamiento digital de señales

El uso de ecuaciones en diferencias permite especificar con precisión los filtros digitales y aplicarlos de forma eficaz. Esto es especialmente importante en los vibrómetros láser Doppler, donde se procesan digitalmente grandes cantidades de datos con precisión y en tiempo real, y la potencia de cálculo es crítica. La precisión matemática y la flexibilidad que ofrecen las ecuaciones en diferencias las convierten en una herramienta indispensable para el desarrollo y la aplicación de algoritmos modernos de procesamiento de señales. Su aplicación permite analizar y manipular señales complejas, mejorando significativamente la calidad y eficacia del procesamiento de señales.

¿Tiene alguna pregunta? Póngase en contacto con nosotros

Recapitulación y perspectivas

 

En resumen, el tratamiento de señales es un campo diverso y profundo que abarca numerosas técnicas y herramientas. Desde la convolución en el tratamiento digital de señales hasta el uso de la transformada de Fourier, el tratamiento de señales es la base de muchas tecnologías y aplicaciones modernas. La adquisición y el tratamiento precisos de las señales son esenciales en muchos campos técnicos y científicos, y se perfeccionan constantemente gracias a la investigación y la innovación continuas.

Otros temas sobre tecnología básica y de medición

Fuente láser
Vibrometría láser
Medición de vibraciones
Efecto Doppler