Ein Ingenieur verwendet ein Laser-Doppler-Vibrometer, um die Schwingungen eines Autos in einem schalltoten Raum zu analysieren. Der grüne Laserstrahl ist auf die Autotür gerichtet, um genaue Schwingungsdaten zu erfassen. Das Auto befindet sich in einer speziellen akustischen Umgebung, die Messungen ohne Störgeräusche von außen ermöglicht.

Signalverarbeitung: Grundlagen, Techniken und Anwendungen

Die Signalverarbeitung umfasst die Analyse und Veränderung von Signalen, um nützliche Informationen für verschiedene Anwendungen zu gewinnen.

Grundlagen der Signalverarbeitung

 

Die Signalverarbeitung ist ein breit gefächertes Gebiet der Ingenieurwissenschaften und der Informatik, das sich mit der Analyse, Veränderung und Synthese von Signalen befasst, um daraus Informationen zu gewinnen. Diese Informationen können in dem Signal beispielsweise in Form von elektrischen, akustischen oder bildgebenden Daten enthalten sein. Der Unterschied zwischen digitaler und analoger Signalverarbeitung liegt in der Art und Weise, wie die Signale verarbeitet werden. Während sich die analoge Signalverarbeitung mit kontinuierlichen Signalen beschäftigt, arbeitet die digitale Signalverarbeitung (DSP) mit diskreten Signalen. Die Verarbeitung von digitalen Signalen ist eine der Voraussetzungen für die heutige digitalisierte Welt und wirkt sich auf fast alle Lebensbereiche aus.

Signalverarbeitung von Sensordaten

 

Daten werden häufig als Zeitsignale von einer Vielzahl von Sensoren aufgezeichnet. Diese Sensoren erfassen physikalische Phänomene wie Temperatur, Druck oder Licht und wandeln sie in elektrische Signale um, die dann weiterverarbeitet werden können. Die Fähigkeit, diese Signale präzise zu erfassen und zu analysieren, ist entscheidend für Anwendungen in der Medizin, der Kommunikationstechnik, der Automatisierung und vielen anderen Bereichen.

Digitale und analoge Signalverarbeitung

Grafische Darstellung der Analog-Digital-Wandlung: Ein analoges Sinussignal wird in ein digitales Signal umgewandelt. Das obere Diagramm zeigt das kontinuierliche analoge Signal, während das untere Diagramm die quantisierte Version des Signals nach der Umwandlung in digitale Werte zeigt.

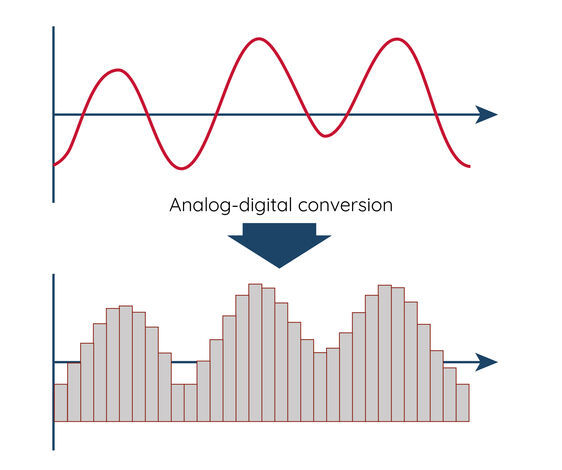
Vor der digitalen Signalverarbeitung werden kontinuierliche analoge Signale durch einen Analog-Digital-Wandler (ADC) in diskrete digitale Signale umgewandelt. Diese digitalen Signale können dann mit digitalen Signalprozessoren oder Computern verarbeitet werden. Die digitale Signalverarbeitung bietet mehrere Vorteile:

 

  • Reproduzierbare und präzise Ergebnisse: Umwelteinflüsse und Komponententoleranzen haben wenig Einfluss auf die Datenverarbeitung

  • Flexible Möglichkeiten: Schnelle Entwicklung und kostengünstige Modifikation der Signalverarbeitung

  • Einfache Implementierung durch die Verwendung bekannter Algorithmen

  • Sichere Speicherung und effiziente Übertragung von digitalen Daten

  • Verbessertes Signal-Rausch-Verhältnis durch Anpassung an die Daten

Innovative Signalverarbeitung im SMART Lab

Grundlagen und Techniken der Signalverarbeitung

 

Algorithmen, zum Beispiel zum Mischen, Filtern, Transformieren oder Steuern eines Signals, bilden die Grundlage der Signalverarbeitung und kombinieren verschiedene mathematische Operatoren und Konzepte, um aus Teilen eines oder mehrerer Signale ein neues Signal zu erzeugen. Einige wichtige Konzepte sind Faltung, Filterung und Fourier-Transformation.

Faltung und digitale Signalverarbeitungsfilter

Die Faltung ist ein mathematischer Operator, der zwei Funktionen kombiniert, um eine dritte Funktion zu erzeugen. In der digitalen Signalverarbeitung wird die Faltung häufig zur Durchführung von Filteroperationen verwendet. Filter können verschiedene Formen annehmen, wie Tiefpass-, Hochpass-, Bandpass- oder Kerbfilter. Sie werden eingesetzt, um unerwünschte Frequenzanteile aus einem Signal zu entfernen oder bestimmte Frequenzbereiche zu betonen. Dadurch werden die Daten bei der Signalverarbeitung verbessert, zum Beispiel durch Glättung oder Rauschunterdrückung.

Verwendung der Fourier-Transformation

Ein wesentlicher Bestandteil der Signalverarbeitung ist die Fourier-Transformation, mit der ein Signal aus dem Zeitbereich in den Frequenzbereich transformiert wird. Diese Technik ist von zentraler Bedeutung, da viele Signale im Frequenzbereich einfacher analysiert und manipuliert werden können. Mit der schnellen Fourier-Transformation (FFT), einer effizienten Implementierung der Fourier-Transformation, können Ingenieure die Frequenzkomponenten eines Signals schnell identifizieren und analysieren.

Die Rolle der Differenzengleichung in der Signalverarbeitung

 

Ein wesentliches Hilfsmittel in der Signalverarbeitung ist die Differenzgleichung. Differenzgleichungen sind rekursive Gleichungen, die den aktuellen Wert einer diskreten Zeitreihe in Abhängigkeit von ihren früheren Werten und den Eingangswerten beschreiben. Sie ermöglichen es, das Verhalten eines Signals systematisch zu modellieren und zu analysieren. In der digitalen Signalverarbeitung werden Differenzgleichungen häufig für den Entwurf und die Implementierung digitaler Filter verwendet, da sie eine mathematisch fundierte Methode zur Beschreibung von Signaltransformationen darstellen.

Mathematische Darstellung

 

Differenzgleichungen werden gewöhnlich in der Form y(n) = ∑k=0Nak x[n - k] + ∑m=1Mbm y[n - m] dargestellt, wobei y(n) der aktuelle Ausgangswert, x(n) der aktuelle Eingangswert,ak und bm die Filterkoeffizienten sind. Diese Gleichung zeigt, wie der aktuelle Ausgangswert durch eine gewichtete Summe der aktuellen und vorherigen Eingangswerte sowie der vorherigen Ausgangswerte bestimmt wird. Durch die Wahl geeigneter Koeffizienten lassen sich verschiedene Filtercharakteristiken wie Tiefpass-, Hochpass-, Bandpass- oder Bandsperrfilter realisieren.

Anwendung bei IIR- und FIR-Filtern

 

In der Praxis ermöglichen Differenzgleichungen die Implementierung von Filtern mit unendlicher Impulsantwort (Infinite Impulse Response, IIR) und endlicher Impulsantwort (Finite Impulse Response, FIR). IIR-Filter, die durch rekursive Differenzengleichungen beschrieben werden, verwenden sowohl vergangene Eingangs- als auch Ausgangswerte und können komplexe Filtereigenschaften mit weniger Rechenaufwand erreichen. FIR-Filter hingegen verwenden nur vergangene Eingangswerte und sind immer stabil, aber oft komplexer zu berechnen.

Bedeutung für die digitale Signalverarbeitung

Durch die Verwendung von Differenzengleichungen können digitale Filter genau spezifiziert und effizient implementiert werden. Dies ist besonders wichtig bei Laser-Doppler-Vibrometern, wo große Datenmengen mit Präzision und in Echtzeit digital verarbeitet werden und die Rechenleistung entscheidend ist. Die mathematische Genauigkeit und Flexibilität von Differenzengleichungen machen sie zu einem unverzichtbaren Werkzeug bei der Entwicklung und Anwendung moderner Signalverarbeitungsalgorithmen. Ihre Anwendung ermöglicht es, komplexe Signale zu analysieren und zu manipulieren, wodurch die Qualität und Effizienz der Signalverarbeitung erheblich verbessert wird.

Haben Sie Fragen? Kontaktieren Sie uns jetzt!

Rückblick und Ausblick

 

Zusammenfassend lässt sich sagen, dass die Signalverarbeitung ein vielfältiges und umfangreiches Gebiet ist, das zahlreiche Techniken und Werkzeuge umfasst. Von der Faltung in der digitalen Signalverarbeitung bis zur Verwendung der Fourier-Transformation ist die Signalverarbeitung die Grundlage für viele moderne Technologien und Anwendungen. Die präzise Erfassung und Verarbeitung von Signalen ist in vielen technischen und wissenschaftlichen Bereichen unerlässlich und wird durch kontinuierliche Forschung und Innovation ständig weiterentwickelt.

Weitere Themen zu Grundlagen & Messtechnik

Laserquelle
Laser Vibrometrie
Schingungsmessung
Doppler Effekt