信号处理:基础、技术和应用
信号处理包括分析和修改信号,以提取各种应用中的有用信息。
信号处理包括分析和修改信号,以提取各种应用中的有用信息。
信号处理是工程学和计算机科学的一个广泛领域,涉及信号的分析、修改和合成,以便从中提取信息。这些信息可以以电子、声学或成像数据等形式包含在信号中。数字信号处理与模拟信号处理的区别在于处理信号的方式。模拟信号处理处理的是连续信号,而数字信号处理(DSP)处理的是离散信号。数字信号处理是当今数字化世界的先决条件之一,几乎影响到生活的所有领域。
数据通常以时间信号的形式从各种传感器中记录下来。这些传感器记录温度、压力或光线等物理现象,并将其转换为可进一步处理的电信号。精确记录和分析这些信号的能力对于医学、通信技术、自动化和许多其他领域的应用至关重要。
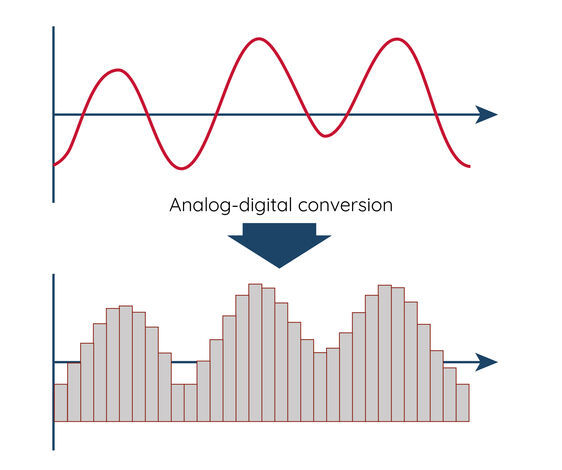
在进行数字信号处理之前,连续的模拟信号要通过模数转换器(ADC)转换成离散的数字信号。然后,这些数字信号可通过数字信号处理器或计算机进行处理。数字信号处理有以下几个优点:
结果可重复且精确:环境影响和元件公差对数据处理的影响很小
灵活性强:信号处理的快速开发和低成本修改
使用已知算法,实施简单
安全存储和高效传输数字数据
通过适应数据提高信噪比
混合、滤波、变换或控制信号等算法构成了信号处理的基础,并将各种数学运算符和概念结合起来,从一个或多个信号的不同部分生成新的信号。一些重要的概念包括卷积、滤波和傅立叶变换。
卷积是一种数学运算符,它将两个函数结合起来,产生第三个函数。在数字信号处理中,卷积通常用于执行滤波器操作。滤波器有多种形式,如低通滤波器、高通滤波器、带通滤波器或陷波滤波器。它们用于去除信号中不需要的频率成分或强调某些频率范围。这可以在信号处理过程中改善数据,例如平滑或抑制噪音。
傅立叶变换是信号处理的重要组成部分,它将信号从时域变换到频域。这项技术至关重要,因为在频域中可以更轻松地分析和处理许多信号。快速傅里叶变换(FFT)是傅里叶变换的一种有效实现方法,通过使用快速傅里叶变换,工程师可以快速识别和分析信号的频率成分。
差分方程是信号处理的重要工具。差分方程是一种递归方程,将离散时间序列的当前值描述为其先前值和输入值的函数。差分方程可以系统地模拟和分析信号的行为。在数字信号处理中,差分方程通常用于设计和实现数字滤波器,因为它们提供了一种描述信号变换的合理数学方法。
差分方程通常以 y(n) =∑k=0Nakx[n - k] +∑m=1Mbmy[n - m] 的形式表示,其中 y(n) 为当前输出值,x(n) 为当前输入值,ak和bm为滤波器系数。这个等式说明了当前输出值是如何由当前输入值和先前输入值以及先前输出值的加权和决定的。通过选择合适的系数,可以实现不同的滤波器特性,如低通滤波器、高通滤波器、带通滤波器或带阻滤波器。
在实际应用中,差分方程可以实现无限脉冲响应(IIR)和有限脉冲响应(FIR)滤波器。IIR 滤波器由递归差分方程描述,同时使用过去的输入和输出值,能以较少的计算量实现复杂的滤波器特性。另一方面,FIR 滤波器只使用过去的输入值,始终保持稳定,但计算起来往往更为复杂。
通过使用差分方程,可以精确指定并高效实现数字滤波器。这一点在激光多普勒测振仪中尤为重要,因为大量数据需要进行精确、实时的数字处理,计算能力至关重要。差分方程的数学精确性和灵活性使其成为开发和应用现代信号处理算法不可或缺的工具。应用差分方程可以分析和处理复杂信号,显著提高信号处理的质量和效率。
总之,信号处理是一个多样而深奥的领域,包含众多技术和工具。从数字信号处理中的卷积到傅立叶变换的使用,信号处理是许多现代技术和应用的基础。信号的精确采集和处理在许多技术和科学领域都至关重要,并通过不断的研究和创新得到进一步发展。
有关基础知识和测量技术的更多主题